Tired of your experiments failing for no apparent reason? Solutions stopped working after just a few weeks?
Sounds like you have a buffer problem!
Whether you’re pulling your hair out and suspect your buffer is the issue, or whether you just need to be able to competently answer “how do buffers work?” before your next meeting—we’ve got your back.
Here’s a short sharp lesson on buffers, how they work, and how to pick the right one for you.
What Is a Buffer?
A buffer is a solution containing acid and a proportionate amount of conjugate base capable of maintaining a stable pH when a small amount of additional acid or base is added to it.
It’s a simple definition, but the underlying chemistry is a little bit complicated. We’ll explain it shortly.
Acids and Bases: A Refresher
Remember that acids donate protons, and bases accept protons.
The stronger the acid, the more readily it will dissociate into protons and anions. Strong bases dissociate readily into cations and proton acceptors.
The strength of an acid or base is measured by its dissociation constant, or pKa. The lower the pKa, the more acidic or basic the molecule.
How Do Buffers Work?
Let’s illustrate this by using the dissociation of HCl to show how compounds can produce acidic or basic products in solution. We can express the dissociation of the strong acid HCl by writing the following equation:
HCl → H+ + Cl–
HCl fully dissociates (breaks apart) into its conjugate base, chloride anions (Cl–), and protons (H+), which are what cause the pH to drop when you add HCl to water.
Because it fully dissociates, there is no dynamic equilibrium between the products and reactants.
That’s to say, if you add any extra protons, they will not recombine with the chloride anions to convert back into HCl. Instead, they will simply add to the overall amount of H+, increasing the H+ concentration in the solution and lowering the pH.
Therefore, HCl is not a buffer because it cannot compensate for changes in proton concentration/pH.
Weak acids don’t fully dissociate in solution. They partially dissociate, and there is an equilibrium between the products and reactants.
We can illustrate this using the dissociation of the weak acid, acetic acid. Acetic acid partially dissociates in solution as per the following equation:
CH3COOH ⇌ H+ + CH3COO–
Here, the products and reactants of the partially dissociated acetic acid are in dynamic equilibrium—the reaction can move back and forth if certain conditions such as temperature, pressure, and concentration are changed.
If the equilibrium is disturbed through the addition of more acid or base, the concentration of the products and reactants change in accordance with Le Chatelier’s principle.
Recall that Le Chatelier’s principle states that when a system at equilibrium is disturbed away from equilibrium, the system will compensate as much as possible to counteract the change.
Any Added protons react with the conjugate base, which is the acetate anion, CH3COO–.
H+ + CH3COO– ⇌ CH3COOH
Any Added base reacts with the conjugate acid, which is the acetic acid.
OH– + CH3COOH ⇌ CH3COO– + H2O
And the overall proton concentration, emboldened and underlined in the overall dissociation equation above, remains almost unchanged.
At some stage, the CH3COOH or CH3COO– will get fully used up and we observe a drastic swing in pH—we’ve exceeded the capacity of the buffer.
Buffers in the Lab
We can achieve a buffering effect using many different weak acids and bases adjusted to a specific pH with a suitable conjugate acid or base.
You will have heard of the common examples used in your lab. Tris, acetic acid, citric acid, sodium phosphate, and HEPES, are some of the more common ones.
Acidic buffers are usually pH-adjusted with their corresponding sodium salt as the conjugate base (citric acid and sodium citrate, etc.) And basic buffers are usually pH-adjusted with HCl (tris base and HCl, etc.) Although there are deviations from this generality.
It is the mixture of weak acid/base with its conjugate partner that enables perturbations in pH to be compensated for. This is because, when a pH-changing chemical is added, the conjugate acid can dissociate into base, and the conjugate base can combine with additional protons.
Why Are Buffers Important to Your Experiments?
A buffer provides a stable chemical environment for your experiments and reactions to take place in!
Once again, let’s use an example to illustrate the importance of buffers and elaborate on the above point.
Suppose you are culturing bacteria in a rich media that can support the growth of a lot of cells. The cells will secrete various chemicals as they grow, live, and die. This is just part of their metabolism and life cycle.
A lot of cells will secrete a lot of chemicals.
Some of these chemicals will be acidic, and some of these chemicals will be basic. Therefore, they will change the pH of the growth medium—unless there is a buffer present to maintain it.
Otherwise, the pH change will be detrimental to cell growth at some point. That’s to say, the cells will die when the pH becomes too low or too high. Not good.
Bonus point for the observant readers—rich cell growth media such as terrific broth are buffered using sodium phosphate!
It’s not just growth media, though. Mobile phases in analytical chemistry, gel loading, enzyme assay, and protein crystallization solutions all contain compatible buffers to maintain their pH.
Buffers and Solution Longevity
There are passive effects that buffers mitigate too. For example, chemicals in your solutions will degrade over time, producing products that alter their pH.
And atmospheric CO2 dissolves in water to generate carbonic acid, making your solutions more acidic over time.
And there’s always that pesky floaty life that starts to grow in old bottles; they will also change the pH of the solution.
Buffers and Species Protonation
A lot of chemicals we are interested in as biologists have different protonation states. And those protonation states can be critical for our experimental design and outcomes.
Take lysine, for example. It has three functional groups that it can donate protons from depending on the solution pH:
- The carboxyl proton.
- The ammonium proton.
- The side chain proton (also ammonium for lysine).
The carboxyl group is acidic by definition, and a solution with a pH > ~2.2 will deprotonate it.
The side chain ammonium group is basic, however. To deprotonate it, we need a solution with a pH > ~10.5. I.e., a moderately basic solution.
Depending on our experimental aims, we might want our lysine analyte to be fully protonated, deprotonated, or somewhere in between.
We can achieve the desired protonation state by using a buffer.
Lysine is a crude example, but SDS-PAGE and ion-exchange chromatography are two techniques in which control over species’ protonation is crucial to success. Protein crystallization is another.
Check out Figure 1 below to see the same point illustrated with the conjugate acids of buffers sodium phosphate and sodium citrate.
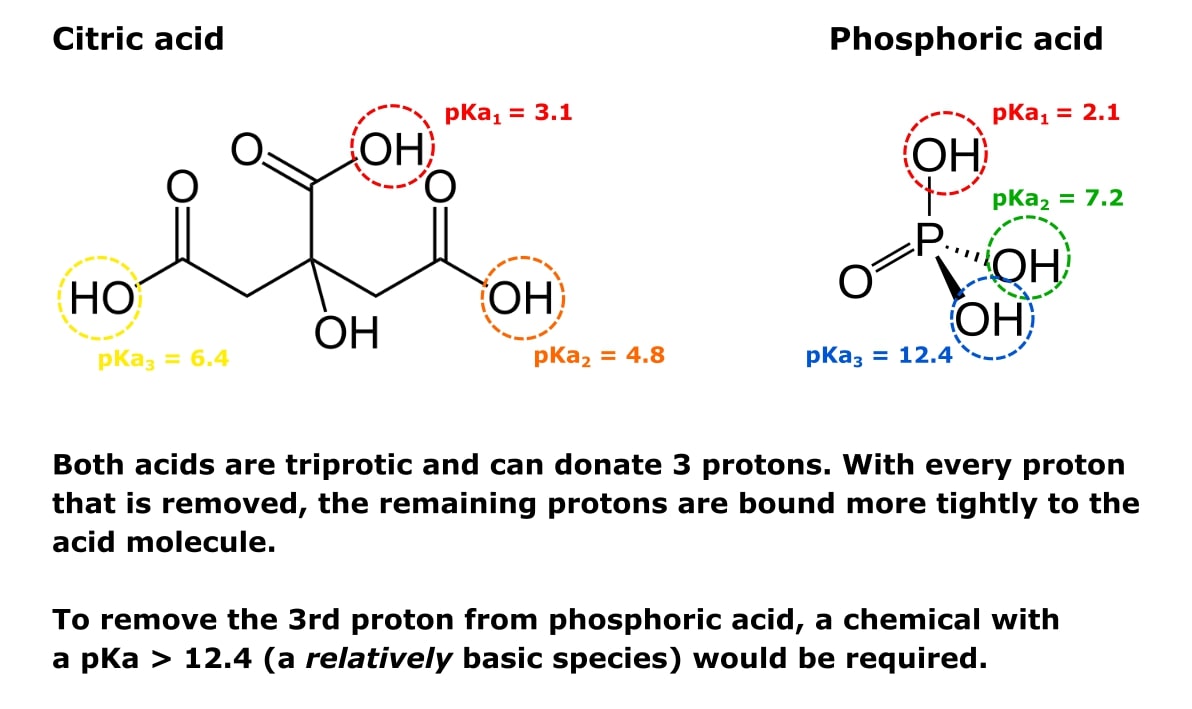
Both acids in this figure are triprotic and can donate three protons. With every proton that is removed, the remaining protons are bound more tightly to the acid molecule. To remove the third proton from phosphoric acid, a chemical with a pKa > 12.4 (a base) would be required.
Mixing mono, di, and tribasic forms of these chemicals together in specific ratios allows us to tailor the pH of the buffer solution.
Buffers in Biology and Biological Buffers
Biological systems have peak activity in a very pH narrow range (at a pH of about 7 most of the time). This is simply because most life on earth is water-based, and water has a pH of 7.
For example, egg whites and seawater have a pH of ~ 8. Blood, sweat, and tears are closer to 7.3. And milk is about 7. Gastric juices, however, are heavy in HCl and have a pH of just below 2.0.
So it’s no coincidence that most biological acids and bases are weak. But even a pH that is only slightly lower or higher than seven can impact your experiments.
Remember that pH and buffer strength are calculated on a logarithmic scale. So choosing a buffer of appropriate acidity/basicity is critical.
How to Choose an Appropriate Buffer
So, you’re convinced. Now you’re going to buffer everything. But how do you select an appropriate buffer? And once you’ve chosen a buffer, how much should you add to your experiment?
Oh, and by appropriate, I mean a buffer that can maintain a pH range that approximately matches your experiment’s intended pH.
As an aside, did I mention that buffers have pH ranges—well, they do! Some have broad ranges and can operate over several pH units. Some have narrow ranges. You’ll know when you’ve exceeded the range of a given buffer because adding extra acid or base will drastically change the pH (the opposite of what a buffer should do).
Anyway, to deduce these two things, you need to know the negative log of your buffer’s dissociation constant, pKa. Usually, you can look this up on the internet. Usually, you have no other choice but to look it up, in fact. But you can calculate it using the following equation if need be:
Ka = [H+][A–]/[HA].
Simply take the negative logarithm of your Ka to get pKa.
To pick an appropriate buffer, select one with a pKa that closely matches the desired pH of your experiment. Simple.
This is because when pH = pKa, 50% of the conjugate acid has dissociated, meaning there is an equal proportion of conjugate acid and base available to react with added H+ and OH–.
And to calculate how much buffer to add to your experiment or how much acid or base to add to your buffer to achieve the desired pH—I’ll keep things simple.
You could get all fancy and rearrange the equation above for the desired term [H+], [A–], or [HA]. Then you could go to the lab and start faffing around adding minute amounts of powder and liquid to your experiment.
Or you could:
- Dissolve a high concentration of your chosen buffer in water.
- Titrate in conjugate acid or base until you achieve your desired pH.
- Autoclave and store it.
- Add this stock solution into your experiments to a sensible concentration.
Simple, eh!
Considerations for Choosing an Appropriate Buffer
We just explained the nitty gritty of choosing an appropriate buffer, but there are other factors to consider. Let’s group these with what we’ve learned already:
- Choose a buffer with a pKa that matches the pH of your intended experiment.
- Choose a buffer that doesn’t react with your analytes.
- Choose a buffer that is compatible with your instrumentation.
- Beware that changing the temperature of the buffer changes its pH.
- Beware that neutralizing HCl with NaOH produces extra NaCl.
And to help you a bit further, here’s a selection of Good’s buffers and their corresponding pKa. [1]
Table 1. A non-exhaustive list of Good’s buffers.
Buffer | pKa |
MES | 6.15 |
Bis-tris propane | 6.80 |
PIPES | 6.82 |
MOPS | 7.15 |
HEPES | 7.55 |
TEA | 7.8 |
Tricine | 8.15 |
Tris | 8.2 |
TAPS | 8.55 |
CAPSO | 9.6 |
CAPS | 10.4 |
There’s More to Learn about Buffers
And that’s the answer to “how do buffers work?” along with a load of extra information that you’ll hopefully find useful in the lab.
It doesn’t end there, though! Why not learn how to design the perfect buffer solution for your experiments or read about what separates good buffers from outstanding ones?
If you want to dive deeper into the technical aspects of buffers and their preparation, watch our on-demand webinar on how buffers work.

Remember—using the correct buffer will lead to more successful experiments.
Take your protein purification game to the next level with our two free eBooks: The Bitesize Bio Guide to Protein Expression and Five Methods for Assessing Protein Purity and Quality.
And be sure to leave any questions in the comments section below!
Originally published April 2012. Reviewed and updated September 2022.
References
- Good NE et al. (1966) Hydrogen ion buffers for biological research. Biochem 5(2):467–77