We all rely on pH, pKa, and pI for a vast amount of our research. But what is pH? How does it relate to pKa and pI?
These numbers fall into that category: “things I learned eons ago, and now I’m too embarrassed to ask what they are.”
Fortunately, reading an article on the internet is discreet. (Imagine if we had to ask somebody the questions we Googled!)
And here at Bitesize Bio, we don’t judge.
Need to quickly re-learn what these parameters are so that you can confidently train an inductee? Been handed an urgent lab task that requires you to fully understand these numbers to do a thorough job of it?
Stick around, be anonymous, and learn the answers to “what is pH?” “what is pKa?” and “what is pI” without ignominy.
A Crash Course on Logarithms
The “p” in pH, pKa, and pI denotes the negative logarithm, to base 10, of the parameter in question.
Logarithms transform a nonlinear series of values into a linear series.
E.g., the logarithm (to base 10) of, 10, 100, 1000, and 10,000 is 1, 2, 3, and 4 respectively.
A quick math rule to jot down in your notebook.
When:
LogXY = Z
Then:
XZ= Y
For example:
Log101000 = 3
So:
103 = 1000
Logarithms make it easier to read and manipulate numbers, the range of which spans several orders of magnitude.
This is achieved by representing all the numbers in question by the number of times a factor needs to be multiplied by itself to equal the original value.
E.g., 10 is a factor of 1000. The number 10 needs to be multiplied by itself 3 times to equal 1000. So Log101000 = 3 and so on.
As such, the logarithm function is the inverse function to exponentiation.
By convention, “log” is taken to mean “log to base 10.”
And remember, the “p” denotes a negative logarithm.
So, at the risk of jumping ahead, a solution with a molar concentration of 10-7 protons has a pH of 7. If the negative sign wasn’t applied to the log function, a solution with a molar concentration of 10-7 protons would have a pH of -7.
So the negative sign is just a fiddle factor that makes the pH scale a positive one.
I know, I know. It’s not a maths blog. But I can’t answer “what is pH?” etc., without explaining logarithms.
What Is pH?
pH is a measure of the acidity or basicity of a solution.
The acidity or basicity of any solution is defined by its concentration of protons.
So, mathematically, pH is the negative log to base 10 of the proton concentration.
In chemistry, the concentration of any species is denoted by writing it in square brackets.
For example, [X] means “the concentration of X.”
Given the above definition of pH, the fact that a proton is simply a hydrogen atom that has lost its only electron (H+), and using the square bracket notation, we can express the answer to “what is pH?” mathematically:
pH = -log10[H+]
And, using the wee bit of algebra presented in the previous section:
10-pH = [H+]
Here’s a handy table so you can see how these two equations relate to one another.
Table 1. The relationship between pH and proton concentration, [H+].
pH | Proton concentration [H+] in M | pH = -log10[H+] | 10^-pH = [H+] |
1 | 10-1 | 1 = -log10[10-1] | 10-1 = [H+] |
2 | 10-2 | 2 = -log10[10-2] | 10-2 = [H+] |
3 | 10-3 | 3 = -log10[10-3] | 10-3 = [H+] |
4 | 10-4 | 4 = -log10[10-4] | 10-4 = [H+] |
5 | 10-5 | 5 = -log10[10-5] | 10-5 = [H+] |
6 | 10-6 | 6 = -log10[10-6] | 10-6 = [H+] |
7 | 10-7 | 7 = -log10[10-7] | 10-7 = [H+] |
8 | 10-8 | 8 = -log10[10-8] | 10-8 = [H+] |
9 | 10-9 | 9 = -log10[10-9] | 10-9 = [H+] |
10 | 10-10 | 10 = -log10[10-10] | 10-10 = [H+] |
11 | 10-11 | 11 = -log10[10-11] | 10-11 = [H+] |
12 | 10-12 | 12 = -log10[10-12] | 10-12 = [H+] |
13 | 10-13 | 13 = -log10[10-13] | 10-13 = [H+] |
14 | 10-14 | 14 = -log10[10-14] | 10-14 = [H+] |
So, the pH scale ranks the acidity of a solution.
What Is pKa?
Now that we have an answer to “what is pH?” let’s move on to pKa.
pKa is the measurement of acidity or basicity of a chemical or functional group.
The acidity or basicity of a chemical or functional group can be defined in two ways:
- The ability to accept or donate a proton.
- The ability to accept or donate a lone pair of electrons.
Remember, electron lone pairs aren’t involved in a bond. These two definitions belong to the respective theories:
- Brønsted–Lowry acid-base theory.
- Lewis acid-base theory.
To be absolutely clear:
- A Brønsted–Lowry acid readily donates a proton.
- A Brønsted–Lowry base readily accepts a proton.
- A Lewis acid accepts a pair of electrons.
- A Lewis base donates a pair of electrons.
It may seem unnecessary to have two definitions, but it is actually quite useful.
For example, the residues histidine, lysine, and arginine are Lewis bases. This is because they can all donate a lone pair of electrons. Histidine from the non-delocalized lone pair on the imidazole side chain; lysine from the terminal amine group, and arginine from the guanidino group.
Hydrochloric acid (HCl) is a strong Brønsted–Lowry acid, whereas sodium hydroxide (NaOH) is a strong Brønsted–Lowry base.
Mathematically, pKa is defined as the negative logarithm of the acid dissociation constant, Ka.
Before going further, let’s have a quick refresher on Ka.
A Refresher on the Acid Dissociation Constant, Ka
We can take any acid and label it “HA” where H is the proton associated with the conjugate base, A.
In solution, HA will dissociate into a free proton, H+, and free conjugate base, A–. Using the squared bracket notation mentioned already, we can write:
HA -> H+ + A–
And given that stoichiometry must be obeyed, using the squared bracket notation described already, we can write:
[HA] = [H+][A–]
When the equilibrium is achieved, the concentrations of products and reactants are no longer changing. So the ratio of the products to reactants is also not changing.
The product:reactant ratio is constant. This is the acid dissociation constant, Ka.
Ka = [H+][A–]/[HA]
The larger the value of Ka, the higher the product:reactant ratio.
That’s to say, the higher the value of Ka, the more free protons there are in the solution.
This, by definition, means the larger the value of Ka, the stronger acid we are dealing with.
Remember—stronger acids have larger Ka values than weaker acids.
pKa Explained Further
Now we know what Ka is, we can understand pKa.
Remember the definition given earlier? pKa is defined as the negative logarithm of the acid dissociation constant.
Or, to put it another way, pKa is to Ka, what pH is to proton concentration.
And we just said that the larger the value of Ka, the stronger acid we are dealing with.
This relationship gets reversed when we take the negative logarithm to calculate pKa.
- Larger Ka—the stronger the acid.
- The smaller the pKa—the stronger the acid.
Confusing for sure, but it’ll sink in.
In summary, pKa is a measurement of how readily a chemical or functional group donates a proton. The more readily it does this, the more acidic the chemical or functional group is.
Every chemical has a unique pKa value (or set of pKa values if it can donate more than one proton).
It’s important to remember that acidity is relative.
If you take a weak acid such as acetic acid and mix it with water, acetic acid will donate a proton. If you mix in add a stronger acid, such as HCl, the acetic acid molecules will start accepting protons donated by HCl. That’s to say, acetic acid will act as a base.
It’s all relative (to pKa!)
For example, look at the triprotic acids citric and phosphoric acid shown in Figure 1.
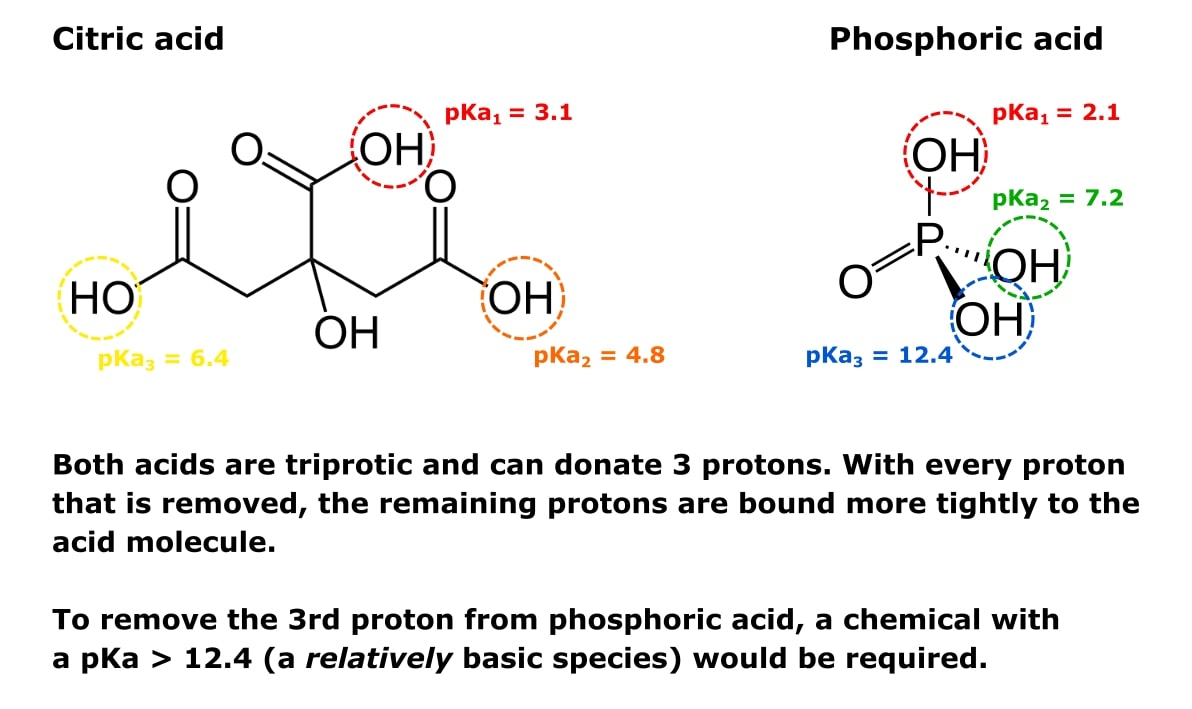
Every molecule of each acid can donate three protons (hence triprotic). So both molecules have three pKa values—one for each proton-donating group one.
When one proton is removed, the other two become harder to remove. That’s why the respective pKa values get higher with each proton removed.
This is also why we can prepare buffer solutions at specified pHs by mixing different ratios of sodium phosphate monobasic and sodium phosphate dibasic.
The monobasic form has two protons remaining and is relatively acidic.
The dibasic form has one proton remaining and is relatively basic.
Useful, eh!
What Is pI?
pI (or isoelectric point) is the pH at which a molecule has no net charge.
Mathematically, it is defined as the mean of the pKa values for a molecule.
Simple!
So, the pI of a protein is determined by the pKa of every amino constituent amino acid.
The situation is complicated somewhat by the fact that proteins fold, however.
While every amino acid has its own pKa (and therefore pI), they vary as a function of how many other amino acids are close to it.
And remember, acidity is relative.
This is one more reason why protein structure is crucial to its function!
The pI for short polypeptides such as those that are just two or three amino acids long is the average pKa for each amino acid.
Bonafide proteins, however, are much more difficult to calculate a pI for.
Fortunately, clever boffins have realized the benefit of calculating the isoelectric point from a primary sequence. This has resulted in useful servers that perform this function!
This is very useful if you want to perform ion-exchange chromatography on your protein sample or do some isoelectric focussing.
Some other facts about the isoelectric point that may be useful to you:
- Most proteins are negatively charged at physiological pH (~ 7.4).
- The pI is also the pH at which the protein is least soluble.
Easy Peasy
Now you tell me, what is pH? Hopefully, you’re clued in with a cogent answer now and can confidently apply what you’ve learned in this article to your day-to-day research!
Still confused? Don’t hesitate to post your questions in the comments section.
Originally written by Andrew Porterfield and published 8 October 2012. Rewritten and republished on February 2022.







