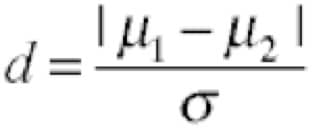Let’s Talk About Stats: Comparing Multiple Datasets

Last week I focused on the left-hand side of this diagram and talked about statistical tests for comparing only two datasets.  Unfortunately, many experiments are more complicated and have three or more datasets.  Different statistical tests are used for comparing multiple data sets.

Today I will focus on the right side of the diagram and talk about statistical tests for comparing more than two datasets.

One independent variable

One-way ANOVA (analysis of variance)

If you are comparing multiple sets of data in which there is just one independent variable, then the one-way ANOVA is the test for you!

ANOVA makes the same assumptions as the t-test; continuous data, which is normally distributed and has the same variance. ANOVA produces an F-ratio from which the significance (p-value) is calculated. You don’t really need to know what the F value is, but simply put it is the ratio of between-group variance and within-group variance. An F-value equal or close to 1 means that there is no significant difference between your data, whereas the higher the F-value, the more likely it is that there is a true difference within your data.

ANOVA tests whether there is a significant difference within your data as a whole, and provides a single p-value, but won’t be able to tell you between which datasets the significance is found. To get more insight into your data and to discover where the significance lies you need to do a post-hoc (which simply means ‘after this’) test.

While the ANOVA is primarily used for comparing multiple sets of data, it can also be used as an alternative to the t-test when comparing two groups of data.

Kruskal-Wallis test

This Kruskal-Wallis test is similar to the one-way ANOVA however it is used when you cannot assume normal distribution or similar variances. As with all non-parametric tests (where no assumptions about distribution and variance are made) this test is less powerful, but more conservative than its parametric equivalent. This test is an extension of the Mann Whitney U test, meaning it is a rank test, but allows for comparison of multiple samples. Like the ANOVA, the result of this test provides the information as to whether there is a significant difference within the data but does not provide the details of this.

Two independent variables

There are often situations in biology where you are looking at the effect of multiple variables on your chosen observation. For example,  let’s say I am comparing the effects of Drug A and Drug B in humans to determine which drug gives a better outcome.  Then I realize that the effects of the drug might be different in males versus females. In this scenario you can analyse the two variables (Drug and sex) simultaneously. This has the benefit of being able to uncover if an association between the two independent variables exists and whether this affects the unknown variable you are testing. For example Drug A may have a great effect compared to Drug B, but only in males. So what tests exist for the analysis of such data?

Two-way ANOVA

You’ve probably guessed that this is simply an extension of the one-way ANOVA and therefore has the same assumptions (to refresh you these are continuous data, approximately normally distributed and equal variance). Like the one-way ANOVA, the two-way also produces an F value that is used to calculate the significance value. In a two-way ANOVA you have three null hypotheses you are testing; the first being that the means of variable one are the same, the second is that the means of variable two are the same, and finally that the two variables do not influence one another.

Scheirer-Ray-Hare

Of course this guide wouldn’t be complete without the provision of a test that is the non-parametric equivalent of the two-way ANOVA.

It is at this point I should admit – I am not a statistician. There appears to be some conflict as to whether or not a non-parametric two way ANOVA is possible, with some people recommending to use a one way non-parametric equivalent (such as the Kruskal-Wallis test) for the two variables separately.

However, one test that claims to be the non-parametric equivalent of a two-way ANOVA is the Schierer-Rare-Hare test. This is an extension of the Kruskal-Wallis test and is therefore similar in the assumptions it makes (i.e. very few about distribution) and is a rank test. This test appears to be a relatively new test in the world of statistics and as alluded to above, is seen as impossible by some. The relative newness of the test also means that is it not widely included in statistics packages. Therefore I would recommend to use this test with caution, and consider curling up in a ball and rocking back and forth for a few hours before seeking the advice of your resident statistics expert.

Post-hoc testing

All of the above tests will tell you if there is any significant difference within your data as a whole, but they won’t tell you between which sets of data the significance lies. In order to delve deeper and uncover this detail you need to apply a post-hoc test. Read more about the different post-hoc tests in my next post.