In the last post I talked about p-values and how we define significance in null hypothesis testing. P-values are inherently linked to degrees of freedom; a lack of knowledge about degrees of freedom invariably leads to poor experimental design, mistaken statistical tests and awkward questions from peer reviewers or conference attendees. Even if you think you know how they work, let’s start from scratch and go through the process.
First an example*; we have four numbers. The mean of these numbers is five.
Pop Quiz: What is the sum of our four numbers?
You should be able to calculate the sum via some nifty reverse engineering.
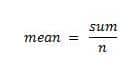
Therefore, the sum must be 20 since there are four numbers and the mean is five.
Now if I tell you the first three numbers:
1. 5
2. 8
3. 4
Pop Quiz: What is the fourth number?
The fourth number can only be three. We know the numbers add up to 20, so no matter what the first three numbers are the fourth must make them add up to 20. This final number is not free to move, its identity is fixed as soon as the other three are determined. So we have three degrees of freedom (n – 1).
The reason we have one degree that cannot move is because we have estimated one parameter – in this case, the mean. Our degrees of freedom are sample size (n) minus the estimated parameters (p). This is the basic formula for determining the degrees of freedom for a given statistical test.
Generally, degrees of freedom are determined by sample size, and with increasing sample size we have increasing degrees of freedom. It’s important that we understand how degrees of freedom (and thus, sample size) affect the significance of p-value testing.
You may recognize the type of table shown below:
Degrees of freedom | a = 0.05 |
1 | 12.71 |
2 | 4.30 |
3 | 3.18 |
4 | 2.78 |
5 | 2.57 |
6 | 2.45 |
7 | 2.36 |
8 | 2.31 |
9 | 2.26 |
10 | 2.23 |
11 | 2.20 |
12 | 2.18 |
13 | 2.16 |
14 | 2.14 |
15 | 2.13 |
It’s used to determine whether a given t-test statistic is significant or not (we’ll be talking t-tests shortly, but for now take my word for it). What the table tells us is the required value of t that will give a significant result at a pre-determined level of alpha. In this case, alpha = 0.05 (the norm for biostatistics). We look down the 0.05 column and line up with the degrees of freedom we have. Let’s start with df = 5; a t stat would need to be at least 2.57 for a significant result. Now raise the df to 15; the t stat would have to be 2.13 for significance. The higher the degrees of freedom, the lower the threshold for a significant result.
Translation: as the degrees of freedom rises, the likelihood of a significant test also rises. Hence the importance of sample size; the more you sample the easier it is to find a significant result.
A warning: we’re all taught statistics using simple, straightforward examples. In any sizable research project, the statistical tests you use will look nothing like what you’ve seen in textbooks. You’ll have multiple variables, sub-sampling, controls… When it comes to degrees of freedom, they get muddled and tricky the more complex your models become. As we get further on in this series and deal with more complex tests, I will draw your attention back to what the appropriate degrees of freedom should be, and the important checks you need to do when calculating complex models in statistical software. Remember the adage: junk in, junk out. It’s up to you to check that the software has correctly attributed degrees of freedom; fail to do this and beware the wrath of peer reviewers.
*This example is cribbed from Michael Crawley’s “Statistics: an introduction using R”. The book comes with my highest recommendation.
Questions? Let us know in the comments section!