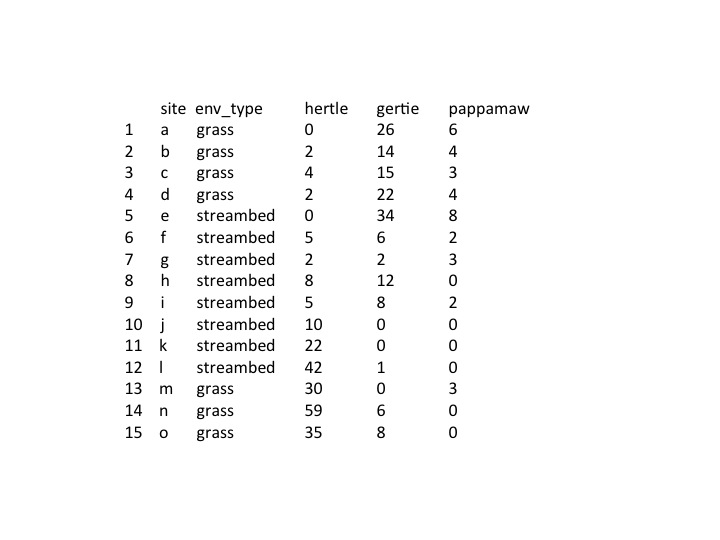
Like many scientists, I don’t consider myself a statistics expert. But I am determined to do things right in my science, and that includes statistics.
In my experience, a lot of scientists who are “scared” of statistics fall into the trap of ignoring the existence of anything beyond a t-test. But using the right method to analyze your data is essential to having confidence in your results, and there are a lot more methods out there than the t-test.
So rather than asking Excel to do a quick t-test for any type of data, I take out my statistics book and read until I’m confident that I have found the right statistical method to use. If you are scared of stats, I hope that this article can convince you to do the same.
Many tests are based on the assumption that the data follows a normal distribution. However, this is often not true for biological data: for instance, you cannot have a negative concentration of a certain protein in your blood. Likewise, very small sample sizes (e.g. n<10) require special treatment. My point here is not to explain to you what you need to do in these cases, but to make you aware that choices need to be made. As an example, let’s take a look at how P-values can be used and misused.
Abusing the P-value
Choosing the right technique is not all there is to it; the way you present the outcome is equally important. I often see people cite P-values in articles without mentioning the effect size found. A P-value in itself says nothing about biological meaning.
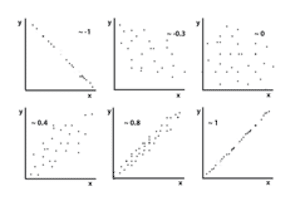
As an example, let’s consider two correlations (associations between two continuous variables). A correlation coefficient ‘r’ describes the degree of ‘straight line’ association between the values of two variables, and it can take any value between -1 and 1 (see approximate examples in the figure). The closer r is to -1 or 1, the more the points in a scatter diagram lie on a straight line. An r close to 0 means there is no specific pattern in the scatter diagram; that is, the two variables are not correlated.
If we only give the significance level of a correlation, we have no idea about the strength of the association, and thus its relevance. If we compare r=0.4 and p<0. 001 with r=0.82 and p=0.06, people might get more excited about the former, due to its high statistical significance.
However, all the former says is that with great certainty (p<0.001: there is only a 0.1% chance that you found this outcome when it is actually not true) there is a correlation coefficient of 0.4, which is in fact not very impressive. On the other hand, p=0.06 is generally considered non-significant, as the level of statistical significance is often arbitrarily set at 0.05. But in this example, a correlation of 0.82 is quite strong, so something seems to be going on here and may be more biologically relevant than something showing a statistically significant correlation of 0.4. To give you a feel for what these numbers mean: R2 (R squared) represents the fraction of the variance of Y that is explained by the variance of X, so roughly from r=0.75 and above we’re really talking business.
With a larger sample size, the correlation of 0.82 might easily have reached statistical significance. Which, by the way, you could have known beforehand had you performed, as one should, a power analysis before starting data acquisition, which tells you the sample size required to detect a biologically significant effect.
This was just one example to make my point about how important it is to correctly present your data. I hope the take-home message is clear: a P-value by itself is never informative!
So when reading an article, do look at the data in graphs and tables, and not just at the P-value and the author’s conclusions; you might find that the author had an optimistic interpretation of his results.
If you have never understood anything of statistics and you don’t want to think about it at all, that’s ok (you’re not the only one!). Ask someone who is not afraid of statistics, ideally before you embark on your project, to ensure that you are collecting the right type of data to answer your questions.
Source:
Altman DG. 1999. Practical statistics for medical research. Chapman & Hall/CRC.
For more information on P-values, check out this article.