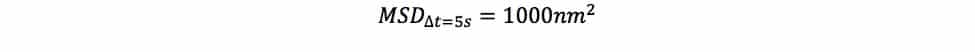Stuff moves. It is useful to study how stuff moves, because motion analysis can tell us a lot about the object that is moving. For example, we can learn if an object’s motion is aimless, diffusive wandering, or directed towards some goal, free to explore the available environment, or restricted to a confined space.
Studying the motion of a single object requires different tools than studying the average motion of a population of objects. Here, I want to introduce you to one of my favorite tools, that mainstay of biophysics, the mean-squared displacement. In this article, I’ll first explain what mean-squared displacement (MSD) is and show you a few of the easiest things to learn from a MSD plot. In a follow-up article, I’ll show you how to make your own plot from a series of measurements of an object’s location.
What kind of object you study doesn’t really matter; I use MSD to analyze motion of proteins and nucleic acids in cells, but the analysis could just as validly be applied to study the motion of individual insects, of amoeboid cells in a petri dish, of a macrophage in a tissue, or really whatever you’re interested in. The only measure required is the object’s location over time.
So what is MSD?
MSD is a statistic that tells you how much your object displaces, on average, in a given interval of time, squared. So if you saw something like this:
You would interpret it as saying that your object displaces 1000nm2 in a 5 second time interval, on average. For easier interpretation, you could take the square root of that, which gives you the “root mean squared displacement.” Then, you’d be able to say that your object displaces about 100nm in 5 seconds, on average.
If it is easier to think about specific data points by taking their square root, why don’t we show root MSD plots instead of MSD plots? Well, some people do. But most still use MSD, because it turns out that looking at motion^2 makes it easy to learn some cool things about the kind of motion the object is doing, as you’ll see below.
You might have noticed I keep saying that MSD describes how much your object displaces, not how much your object moves. This is because usually when you take movies of your object, there is time between the frames. And though you can measure the difference in the object’s position between two frames (i.e. displacement), you don’t really know how much the object moved in that time. For all you know, it may have traveled to the sun and back when your camera wasn’t looking.
It’s also good to keep in mind that MSD is a mean. Your object might have moved 1 nm in one 5 second interval and 1000 nm in another 5 second interval and have the same MSD as an object that moved 500nm in both 5 second intervals. It’s important to look at the standard deviation of MSDs to see how consistent the displacements are.
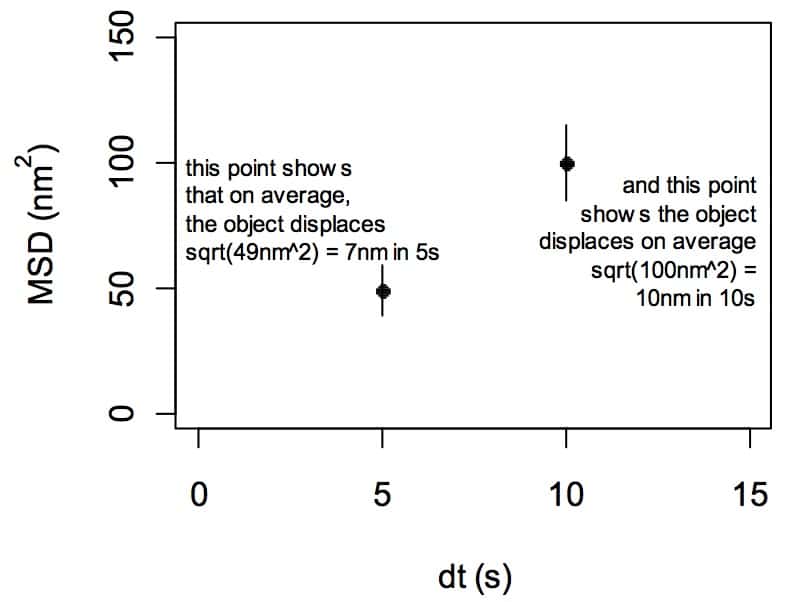
So MSD tells you how much your object displaced in a given interval of time. That’s great, but the really cool thing about MSD is what you can learn when you look at graphs that show many MSD data points over increasing intervals of time. Let’s do that:
The x-axis is what frequently trips people up: the x-axis in in units of a time interval. Often, this is represented as delta-t, a change in time (although sometimes confusingly is just represented as “time”). People often see a “t” or an “s” on the x-axis and then assume the plot is showing a time series. IT IS NOT A TIME SERIES! The x-axis shows time intervals. I cannot stress this enough.
Now that you know what MSD is and the axes, let’s briefly go through the four main things you can detect with a fast glance at an MSD plot. The details behind the following truths are a bit beyond the scope of this article, but can be found in the primary lit.
1. Diffusion
If the MSD plot follows a linear trend, then the object whose motion you are observing moves diffusively; i.e. without direction, as in a random walk. For example, an unbound GFP particle will move diffusively through a cell’s cytoplasm.
2. Active motion
If the MSD plot does not follow a linear trend but instead follows an increasing slope, then the object exhibits directed motion. For example, the motor protein dynein moves along microtubules in a directed fashion, always going from the “plus” end of microtubules to the “minus” end.
3. Constrained motion
If the plot plateaus, then the motion of the object is constrained. Furthermore, the square root of the height of the plateau (minus error) defines the size of the region of constraint. For example, if you labeled a centromere in a budding yeast cell, it could never move outside of the nucleus, and this would be reflected in an MSD plot by a constraint likely with the plateau at the height of the diameter of the nucleus, squared.
4. Measurement error
The intercept of an MSD plot is the measurement error (which can include a number of sources, including microscopy errors and errors in particle tracking in your image analysis software). This makes intuitive sense: the intercept of an MSD plot is where the time interval = 0. Since an object can’t move in zero time, the intercept must reflect measurement error.
With this foundation, you’re equipped to do a basic interpretation of MSD plots. Keep in mind that while we have learned a lot from a simple plot, we can go deeper still, and learn all sorts of cool things like mechanical properties of molecular polymers. Stay tuned for the follow-up, when we learn to make MSD plots from a time series of object locations!