In previous articles, I’ve primed you on hypothesis testing and how we are forced to choose between minimising either Type I or Type II errors. In the world of the null hypothesis fetish, the p-value (p) is the most revered number. It may also be the least understood.
The p-value is the probability, assuming the null hypothesis is true, of obtaining a test statistic at least as extreme as the one calculated from the sample data. In English: how small is the probability that we get this answer, or one more extreme, if the null is in fact true?
If p is high, there is a high likelihood of obtaining said result when the null is actually true, therefore we would choose not to reject the null hypothesis. Vice versa, if p is sufficiently small, the probability of the null hypothesis being true is minimal enough as to reject the null and accept our alternative hypothesis.
Which leads to the million dollar question: what is sufficiently small enough to warrant rejecting the null hypothesis?
Biologists have settled on an acceptable threshold of p = 0.05. In human speak, if the chance of getting our test statistic (if the null hypothesis were true) is less than 5% we feel satisfied in rejecting it and concluding that the alternative hypothesis is true. In other academic circles, a p-value of 0.10 may be acceptable, or a p of 0.01 may be insisted upon.
I’ve sat through many conference presentations where a researcher has deplored their p = 0.06 result and claimed it was “almost significant”. Perhaps it is in human nature that once we have drawn a line in the sand we believe it to be permanent. But the 5% line is arbitrary, and one issue with null hypothesis testing is that it creates this yes/no dichotomy that fails to allow for the blurred edges of the natural world. Sir Ronald Fisher, the patriarch of null hypothesis testing, argued that fixed significance levels were too restrictive and researchers should use a significance level appropriate for their study. Should you ever find yourself in the situation with a p-value of 0.06, put your common sense hat on and ask, if 5% significant, why is 6% not?
At the start of this article I claimed that p-values are misunderstood. Let’s consider what a p-value isn’t.
A p-value is not the probability of a given result being due to chance
Rather, it indicates the long-run probabilities of getting such our result, or one more extreme, if the null hypothesis is true and we take multiple samples.
A p-value is not the probability of the null hypothesis being true, given the data
This may seem semantic, but it does make sense. If you are familiar with conditional probabilities (e.g. P(A|B)), the probability of A, given B has already occurred) you could envision it like this:
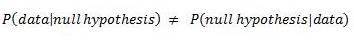
That is to say, the probability of the data, given the null hypothesis is true, is not the same as the null hypothesis being true given the data. In fact, without getting into Bayesian analysis we cannot assign a probability to the null hypothesis being true. We are only sampling from our data set, which allows us to assign probabilities to the data. The null hypothesis remains the same throughout our sampling, which means we cannot calculate a probability related to it.
I hope this has cleared up some of the finer points of p-values for you. Please feel free to leave comments with any questions or concerns.







