Basic Statistics for Flow Cytometrists – Part 1

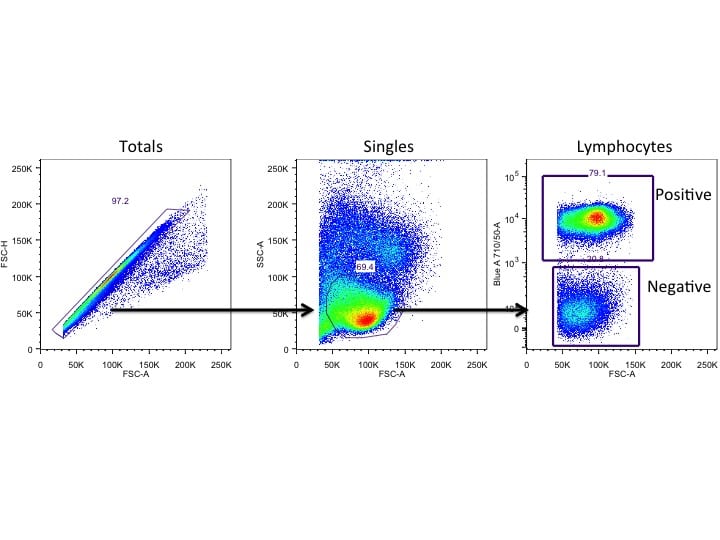
Part of my job in running a core flow cytometry facility is to make sure that the experiments that my users run have been optimised. But that optimisation can be split up into several areas. The first area is experimental planning: What do you want to know? Can you do this by flow cytometry? And if the answer is yes, then how do we design the optimal experiment.

Careful Experimental Design

This brings us to experimental design – having a knowledge of the cytometer you are going to use, its lasers and optical filters is crucial. An experiment will only be as good as your sample preparation and the readiness of your cytometer, so be prepared to spend time perfecting your staining technique and ensuring that your cytometer is optimised. And at the end of your experiment, you need to ensure that you only look at the cells you want to look at, so careful consideration of controls, gating and derivation of appropriate numbers will be just as important as anything that has gone before.

Importance of Statistics

With careful planning you can design and perform an optimal experiment without too much pain. However the journey does not end there – we also have to ensure that we get the right numbers out of the data to answer the question we first posed. Sometimes it is possible to have a great set of data but then stumble at the statistical analysis stage. If, like me, the merest mention of the word ‘statistics’ is enough to make you tremble and lose all sense of logic then here is a basic guide to the statistics we can glean from flow cytometry data and what they are useful for.

Statistics for Flow

Statistics can be descriptive or they can be inferential. As the name suggests, descriptive statistics are the ones we can use to describe our flow data and the ones that allow us to test our hypothesis e.g. is there an increase or decrease in a particular population. Inferential statistic are the ones we used to infer whether our experiment is a representative sample of a whole population.

Descriptive statistics

These are not as scary as you may think as they are the descriptors that allow us to summarise data and the most common examples are:

A Percentage Positive

Easy when we have some cells that express a marker and others that don’t – as long as we have made sure we have the correct control we can say that x% of our cells are expressing a particular marker.

A Measure of Central Tendency

We can use descriptors such as the mean or median (or less often the mode) of a distribution. These will be useful when comparing overlapping distributions, as we will be considering the entire population rather than just a part of it.

Data Spread

This may be measured by the standard deviation or more commonly a coefficient of variation, which allows us to have an idea of the dispersion of the data (the higher the value, the more variance it contains).

Separation Distance

This combines looking at means (or medians) of populations with looking at the data spread.

Fold Over Background

If we ensure that we are comparing like with like, we can calculate the ratio of two distribution signals.

Inferential Statistics

These are used to draw conclusions from the data and we need ensure that we have made sufficient measurements of samples to allow us to get information about the whole population. We want to use statistical tests to make judgements about our experiment, e.g. does our new drug increase cell death in a population? To do this we will use the numbers we get from our data (the descriptive statistics) and apply a statistical test. There is a large range of tests available and the ones we use will depend to an extent on the questions asked as well as our knowledge of the data. In general, we assume that the numbers we get from the flow files are distributed in a Gaussian manner but if we know they are not there are non-Gaussian tests (usually using a ranking of data). In general, if data is assumed to be Gaussian, we would use parametric tests such as a t-test when we want to compare two groups or an analysis of variance (ANOVA) if we have more than two groups. If we are assuming a non-Gaussian distribution, we use a non-parametric test – when we have two groups we would use something like the Wilcoxon test, for more than two a Kruskal-Wallis test. Each of these statistics would need an article on its own, so we have put so in the coming weeks we are covering each of these in articles in the flow cytometry channel– stay tuned!